Учет почвенных беспозвоночных в пробах

При учете почвенных беспозвоночных в пробах общепринятых размеров мы часто сталкиваемся с таким положением, когда большинство проб содержит минимальное число особей или вовсе пусты.

Кривая распределения частот принимает вид, показанный на рисунке. В этом случае мода приходится на минимальное обилие в пробе и далеко отстоит от медианы. Такую гистограмму могут давать многие распределения (в частности, распределения Пуассона). Если распределение особей случайное, то увеличивая размер пробы, мы увеличиваем среднюю, а в случае большой средней случайное распределение аппроксимируется нормальным (Урбах, 1964). В любом другом случае увеличение размера проб не дает приближения к нормальному распределению.
 

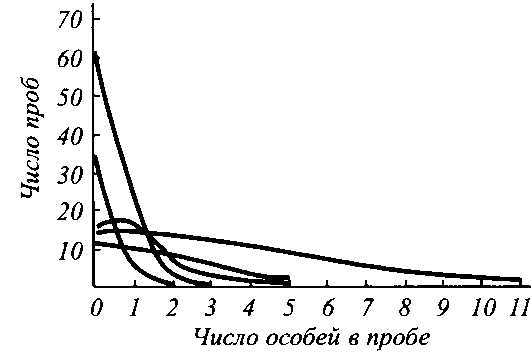
Несколько примеров отрицательного биномиального распределения частот различных видов коллембол и панцирных клещей (по: Чернова, Чугунова, 1967).

В почвенно-зоологических исследованиях определенный размер проб применяется для учета одновременно большого числа видов и групп с разной численностью. Кроме того, размер проб часто диктуется техническими соображениями, например, при учетах в эклекторах. Эти обстоятельства весьма ограничивают использование вариационно-статистических показателей, большинство из которых в строгом смысле применимы лишь при нормальном распределении величин. Эти трудности преодолеваются путем нормирующих преобразований, разработанных для каждого распределения.

Часто численность мелких почвенных животных, таких как коллемболы, клещи, а тем более нематоды, варьирует в очень больших пределах. Так, число особей отдельных видов коллембол в пробах 5x5 см может колебаться от 0 до нескольких сотен. В силу этого иногда невозможно сгруппировать непосредственно цифры вариационного ряда. В таких случаях весь ряд полученных цифр разбивают на классы. Например, если животное встречено в пробах от 1 до 30, то полученные цифры можно разбить на классы: 1 - 5, 6 - 10, 11 - 15 и т.д.

Подсчитав число проб с каждым из классов, можно построить гистограмму. На оси ординат откладываем классы обилия, на оси абсцисс - частоты. Классовый интервал (в данном случае - 5 особей) может быть самым различным, что зависит от уровня численности, размера проб и от целей обработки. Чаще всего выделяют 5-7 классов. Обычно классовые интервалы бывают равные по всему ряду, что увеличивает возможность дальнейших математических операций. Однако иногда можно использовать шкалу с разными интервалами. Так, ногохвостка Folsomia diplophthalma в тундре встречена в пробах (всего 100 проб) в количестве от 0 до 160 особей. Однако подавляющее число проб содержало от 1 до 40 особей, всего 6 проб - свыше 40. Вероятно, в этом случае интервал от 40 до 160 целесообразно объединить в один класс. Группировка учетных данных по классам обилия широко используется для различных целей в почвенной зоологии. Это сильно облегчает анализ количественных материалов.