Верификация модели естественного развития насаждений

Для верификации работы модели было поставлено несколько компьютерных экспериментов. В одном из них с помощью модели естественного развития были получены таблицы хода роста смешанных елово-березовых насаждений, далее их сравнили с таблицами, построенными на основе реальных данных о росте смешанных насаждений (Загреев и др., 1992).

Моделирование роста смешанных насаждений проводили на основе таблиц хода роста одновидовых еловых и березовых насаждений. Результаты показаны на рис. 10.6. При моделировании роста смешанных насаждений среднее отклонение расчетных данных от натурных составляет 3,4%, максимальное - 5%, что позволяет говорить об адекватной работе прогнозного комплекса FORRUS-S. Аналогичные результаты получены в этом эксперименте для других параметров древостоя, включая сумму площадей сечений по видам.

Моделирование развития лесных насаждений при расчете условий освещения элемента моделируемого пространства обязательно требует учета пространственного окружения. Для исследования значимости этого фактора были проведены две серии компьютерных экспериментов. В первой серии модель естественного развития настроена на статичное расположение Солнца сверху, т.е. фиксированное расположение источника света - аналог моделирования светового потока в gap-моделях (Botkin, 1993; Botkin et al., 1972; Leemans, Prentice, 1989; Pacala et al., 1995; Shugart, 1984, 1992). Во второй серии модель использует приведенный в главе 1 алгоритм расчета движения Солнца по небосводу. При этом задается естественная интенсивность свечения Солнца в разные часы суток, учитывается прямая и рассеянная радиация и влияние окружающего древостоя на уровень освещенности моделируемого элемента. Для моделирования использовано порослевое насаждение 40-летнего дуба со средней высотой 16,6 м. Поставлена задача получить прогноз развития культур дуба, посаженных на вырубке внутри названного насаждения. Моделировались котловинные рубки разной площади и лесосеки разной ширины. В первой серии экспериментов все исследованные комбинации рубок приводят к одному и тому же результату: культуры дуба развиваются в соответствии с заданным бонитетом (в данном случае равным единице). На 60-м году культуры дуба достигают высоты 22,1 м, а порослевые 100-летние насаждения дуба - 26 м. Таким образом, в этой серии экспериментов высота окружающего древостоя не оказывает влияния на развитие культур, что противоречит натурным наблюдениям.

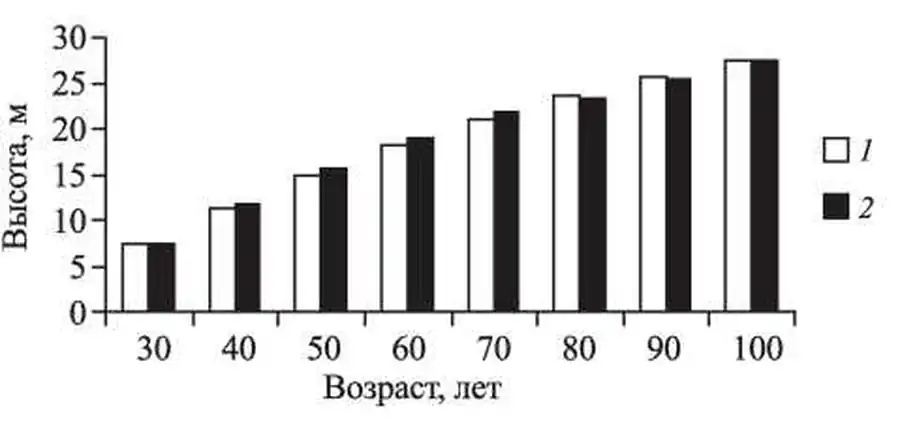
Ход роста в высоту древостоев ели:
1 - средняя высота деревьев разного возраста, полученная по таблицам хода роста смешанных елово-березовых насаждений; 2 - средняя высота деревьев разного возраста, рассчитанная в результате моделирования.

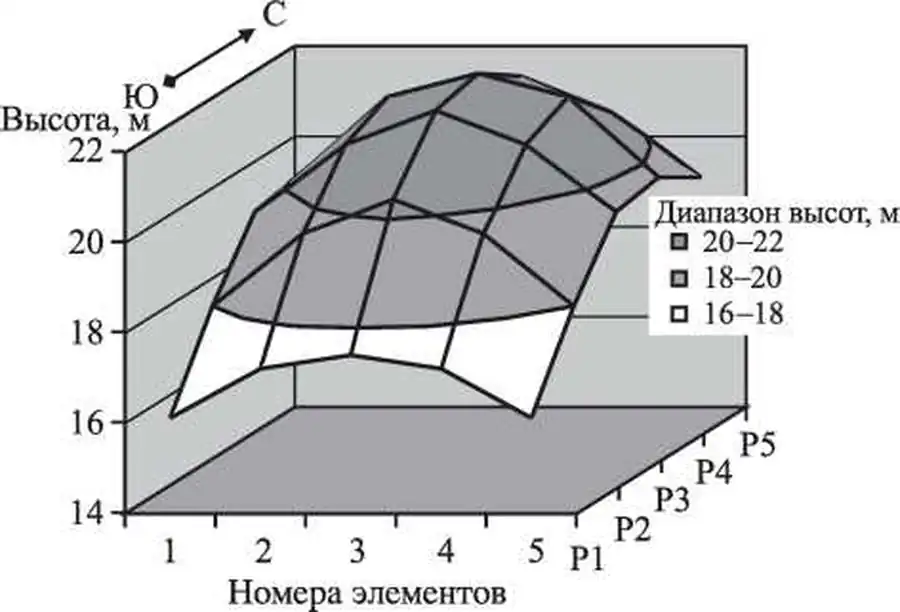
Зависимость высоты 60-летнего дуба от положения в окне котловинной рубки. Р1...Р5 - ряды данных, соответствующих 1...5 рядам ячеек.

Вторая серия экспериментов демонстрирует влияние окружающего древостоя на развитие культур. Например, в окне котловинной рубки размером 270 кв.м за 60 лет культуры дуба достигают высоты 16 м, т.е. отклонение значений, полученных для сравниваемых серий компьютерных экспериментов составляет на 6,1 м меньшее, чем в первой серии (или 38%). Эксперименты с моделированием разных размеров котловинных рубок (от 270 кв.м до 2500 кв.м), лесосек разной ширины (от 16 м до 80 м) и направления (Север-Юг, Запад-Восток) показали, что с увеличением размеров вырубки влияние окружающего насаждения на рост культур уменьшается. На рис. 10.7 показана зависимость высоты 60-летнего дуба от положения в окне, полученная в результате моделирования котловинной рубки размером 83,5 м х 83,5 м (5 элементов х 5 элементов). В этом случае высота дуба в разных частях окна изменяется от 16 до 22 м, причем высота дуба в южной части окна намного меньше его высоты в центральной и северной частях окна, что связано с затенением от полога леса, окружающего окно.

Проведенные исследования позволяют заключить, что дар-модели не рекомендуется использовать для моделирования динамики древостоев на вырубках небольших размеров. Решение этих задач успешно реализует комплекс программ FORRUS-S.