Алгоритм имитационной модели древесной синузии лесного ценоза

Набор положений оказался достаточным для получения в модели непрерывно меняющейся во времени мозаики локальных неоднородностей пространства. Характер этой мозаики (узор) и ее динамичность зависят от ограничений, которые накладываются на линейные размеры ячеек, длительность существования каждого состояния, величины циклов, направления переходов из одного состояния в другое. Именно в таких ограничениях отражаются видоспецифичные различия онтогенетических и экологических параметров древесных видов.

Для исследования динамики многовидовой разновозрастной древесной синузии целесообразно использовать метод имитационного моделирования. Выбор метода обусловлен тем, что закономерности развития древесной синузии описываются большим числом параметров, представленных в таблицах, графиках и элементарных математических зависимостях. Кроме того, учет межвидового биологического и экологического взаимодействия плохо подвергается формализации и требует проверки многочисленных логических условий и ограничений. Выбору данного метода способствует также и то обстоятельство, что модель предопределяет рекурентность алгоритма расчета параметров прогноза развития древесной синузии.

Большинство моделей динамики лесных ценозов состоят из двух подмоделей: особи и ценоза в целом (Оя, 1985). Это определяется тем, что часть параметров зависит от индивидуальных свойств растений, а часть - от их взаиморасположения. Предлагаемая модель не является исключением.

Составлен алгоритм модели многовидовой разновозрастной древесной синузии, на основе которого написана моделирующая программа. Для работы модели необходимо задать эмпирические видоспецифичные функции онтогенетического состояния, такие как прирост в высоту за один шаг моделирования; диапазон фотосинтетической активности; изменение площади кроны; коэффициенты прозрачности кроны; а также возрастные и габитуальные ограничения (предельный возраст перехода в следующее онтогенетическое состояние, максимальный и минимальный радиусы кроны).

Необходимо отметить, что для каждого элемента могут быть заданы параметры, изменяющие темпы роста произрастающих в них особей. Этим самым можно моделировать разнообразные почвенные и гидрологические условия, а также возможные изменения структуры и плодородия почвы, которые очень тесно связаны с сукцессиями растительности.

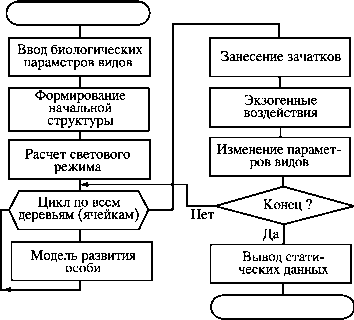
Структура модели древесной синузии

В предлагаемой модели рассчитываются прямая и рассеянная солнечная радиации. При движении солнца по небосводу его положение однозначно описывается его высотой и азимутом, временем стояния и интенсивностью прямой радиации (РА), поступающей на горизонтальную поверхность. При этом следует учитывать число солнечных дней в течение вегетационного периода. Для определения влияния рассеянной радиации солнца весь небосвод делится на фиксированное число зон с одинаковой светимостью и предполагается, что рассеянная радиация (Rj) поступает к земле из центра этих зон.

Освещенность исследуемой ячейки определяется по формулам.

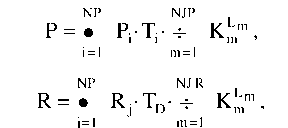
Где Km - коэффициент прозрачности m-й ячейки, через которую проходит свет; Lm - длина пути, проходимая лучом в этой ячейке; - время, в течение которого солнце находится в каждой точке небосвода при расчете прямой радиации; TD - средняя длительность светового дня в течение вегетационного периода; NP - число положений солнца, для которых рассчитывается прямая радиация; NR - число зон небосклона, для расчета рассеянной радиации; NJP, NJR - число ячеек, через которые проходит свет при расчете прямой и рассеянной радиаций, соответственно.

Суммарное дневное поступление солнечной радиации к ячейке определяется по формуле

Ст = Р + R.

Более подробно алгоритм расчета фотосинтетически активной радиации и результаты пробных расчетов представлены в работе С.И. Чумаченко (1993).

После расчета доступной ФАР для всех ячеек осуществляется последовательная их обработка с использованием модели развития особи в условиях конкуренции. Счет начинается с самых высоких деревьев, так как они в большей степени влияют на формирование светового режима.

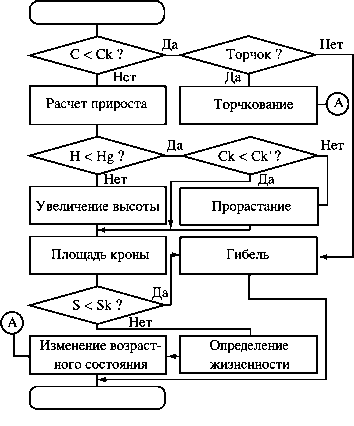
Структура модели развития особи в условиях конкуренции:
С - доступная ФАР рассматриваемого дерева; Ск - значение ФАР в точке компенсации на кривой фотосинтеза; Ск' - то же для рядом стоящего дерева; Н - ожидаемая высота особи; Hg - высота нижних ветвей дерева, занимающего верхнюю ячейку над рассматриваемым; S - площадь кроны; Sk - предельно допустимая площадь кроны

Алгоритм развития особи в условиях конкуренции позволяет моделировать следующие процессы:

а) рост дерева в зависимости от доступной ФАР, от заданных в модели видоспецифичных возрастных темпов роста и от возможности занять более высокий слой ячеек;

б)    изменение площади кроны при наличии свободного пространства в непосредственной близости от особи;

в)    смерть особи, которая может наступить в случае снижения освещенности кроны ниже точки компенсации на кривой фотосинтеза, при недостатке площади питания (заданной минимальной площади кроны) и при длительном угнетении.

После обработки всех ячеек моделируемого пространства имитируется процесс заноса зачатков. Учет пространственной структуры позволяет рассчитать число зачатков, достигающих заданной ячейки в зависимости от наличия генеративных особей и расстояния до них.

После этого моделируется отмирание особей как в экстремальных условиях (массовое размножение различных фитофагов, болезни, сильные морозы, засухи и т.д.), так и при антропогенных воздействиях, например при разнообразных рубках.

Кроме того, в модель заложена возможность изменения биологических характеристик моделируемых видов, например, для моделирования глобальных и региональных изменений экологической обстановки (загрязнения атмосферы и почвы), мощных антропогенных воздействий (осушения болот, изменения уровня грунтовых вод и т.д.), изменения климата, влияния последствий болезней леса.

В качестве результатов моделирования исследователь получает статистические данные по контролируемым в модели параметрам: онтогенетическому состоянию и абсолютному возрасту; суммарной площади, занимаемой каждым видом в любом онтогенетическом состоянии; средней площади кроны в генеративном состоянии; высоте особи и пр.